The development of efficient techniques for the characterization of quantum systems is crucial for the development of quantum technologies for communication, computing, sensing and simulation. As the complexity of quantum states and dynamics increases exponentially with their size, however, their full description becomes intractable and even approximations are often challenging.
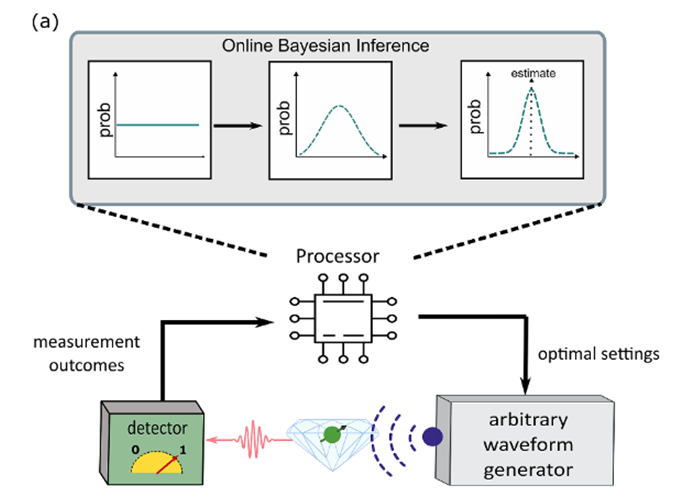
Our group, in collaboration with thereotical quantum physicists (Erik Gauger) and experts in statistical learning (Yoann Altmann), develops novel automated tools to characterise quantum systems, learning the processes (and the associated rates) governing their dynamics. We are particularly interested in artificial intelligence methods that can ‘advise’ experimentalists on the optimal experiments to gain information on a system, for example to distinguish between alternative models that might explain the same datasets. The toolbox we develop is then applied in Quantum Sensing experiments. For a general overview of this research field, you can read our review on “Learning Quantum Systems” (Nature Reviews Physics, 2023 – also available on arXiv).

Learning models for unknown quantum systems. We develop algorithms, utilising a variety of statistical tools such as Bayesian inference, neural networks, graybox models, to automate the extraction of physical models from experimental data in a reliable, robust, and interpretable form. This is an important challenge for both fundamental scientific discoveries and technological applications, for example to propose explanations for experimental data and suggest alternative interpretations that researchers may have not have originally envisioned. We apply these algorithms to a variety of physical systems, ranging from quantum optics to superconducting circuits.

Optimising quantum experiments and quantum sensors. We develop automated systems to advise experimentalists on the optimal experiments to perform in a given setting, for example to distinguish between degenerate models for an unknown quantum systems, or to minimise data acquisition time.

For more information on this work, please contact Prof Cristian Bonato